코학다식
[백준/BOJ/C++] 11657번 :: 타임머신 본문
그래프에서 최단 경로를 찾는 알고리즘 중 하나인 벨만-포드 알고리즘으로 풀 수 있는 문제였다. 주의해야 할 점은 오버플로우가 발생할 수 있기 때문에 거리 배열의 타입을 long long으로 선언해 주어야 한다는 점이다.
Bellman-Ford's Algorithm
어떤 경로든 최대 ||V|| - 1개의 간선으로 이루어질 수 있으므로 모든 간선을 ||V|| - 1번 확인하면서 모든 정점의 최단 거리를 갱신하는 알고리즘이다. 한 개의 정점에서 시작해 모든 정점으로 가는 최단 경로를 찾는다. 간선이 E개, 정점이 V개일 때 각 간선을 ||V|| - 1번 확인하므로 시간복잡도는 O(||V|| ||E||)가 된다. 음수인 간선이 있어도 사용할 수 있다. 아래의 예시에서 시작하는 정점은 S이다.
시작점으로부터 모든 정점의 최단 거리를 매 반복마다 갱신해 준다. 시작점에서 바로 도달하는 경로나 다른 정점을 거쳐서 도달하는 경로가 없는 경우에는 갱신이 불가능하므로 무시하고 그대로 진행해 주고, 갱신이 가능한 경우에는 최단 거리를 찾아 갱신한다. 가령, 기존의 최단 거리가 10인데, 다른 정점을 거쳐서 오는 다른 경로의 거리가 8이라면 후자로 최단 거리를 갱신해 준다.
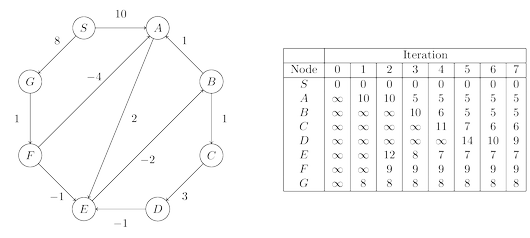
만약 모든 간선이 음수인 가중치를 가지는 등의 몇 가지 경우에서는 간선을 확인할 때마다(루프를 한 번 돌 때마다) 최단 거리가 갱신될 수 있다. 이 경우 최단 경로를 구성하는 노드 수가 ||V|| -1보다 커지게 되는데, 이를 음수 사이클이라고 한다.
풀이
벨만-포드는 코드를 보면서 이해하는 게 더 이해하기 쉬운 것 같다.
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
using pil = pair<int, long long>;
long long INF = 20000000000000000;
vector<long long> dist(501, INF); // 최단 거리를 저장하는 배열, 처음에는 아주 큰 값으로 초기화
vector<pil> graph[501]; // destination, cost
int main() {
dist[1] = 0;
int n, m;
cin >> n >> m;
while(m--) {
int u, v, c;
cin >> u >> v >> c;
graph[u].emplace_back(pil(v, c));
}
for(int i = 1; i < n; i++){ // ||V|| - 1번 반복
for(int u = 1; u <= n; u++) { // 모든 간선에 대해서
if(dist[u] == INF) continue; // 시작점에서 방문하지 못하는 경우 넘어간다
for(pil v : graph[u]) { // 방문 가능한 경우 최단 거리를 갱신한다
dist[v.first] = min(dist[v.first], dist[u] + v.second);
}
}
}
bool flag = false; // 무한히 시간을 오래 전으로 돌릴 수 있는 경우, 즉 음수 사이클이 존재하는지 검사
for(int u = 1; u <= n; u++){ // 반복을 한 번 더 수행하면서
if(dist[u] == INF) continue;
for(pil v: graph[u]) {
if(dist[v.first] > dist[u] + v.second) { // 최단 거리가 갱신되는 경우
flag = true; // 음수 사이클이 존재한다는 것을 알 수 있다
break;
}
}
}
if(flag) cout << -1;
else {
for(int i = 2; i <= n; i++){
if(dist[i] == INF)
cout << -1 << "\n" // 경로가 존재하지 않는 경우
else
cout << dist[i] << "\n"; // 경로가 존재하는 경우 최단 거리
}
}
return 0;
}'Algorithm > Problem' 카테고리의 다른 글
| [프로그래머스/C++] 베스트앨범 (0) | 2020.09.03 |
|---|---|
| [프로그래머스/C++] 위장 (0) | 2020.09.02 |
| [프로그래머스/C++] 섬 연결하기 (0) | 2020.09.01 |
| [백준/BOJ/C언어] 2470번 :: 두 용액 (0) | 2019.09.25 |
| [백준/BOJ/C언어] 10814번 :: 나이순 정렬 (0) | 2019.09.23 |
Comments

