코학다식
[알고리즘] DFS와 BFS에 대해 알아보기 본문
안녕하세요. 이번 글에서는 기초적인 그래프 operation인 DFS와 BFS에 대해 알아보도록 하겠습니다.
본격적으로 DFS와 BFS에 대해 알아보기에 앞서, 먼저 그래프에 대해 간략하게 알아보도록 하겠습니다. 그래프와 DFS, BFS에 대한 설명은 Fundamentals of data structures in C 2nd edition의 설명을 참고하였습니다. 예제 코드는 C언어를 사용합니다.
Graph
그래프[G]는 자료구조의 일종으로 두 집합으로 이루어져 있습니다. 유한한, 그러면서 빈 집합이 아닌 정점들의 집합[V(G)]과 정점들의 쌍인 간선들의 집합[E(G)]이 그래프를 이루어는 두 집합입니다. 참고로 context에 따라 차이가 있으나 대부분 정점이 존재하면서 간선이 없는 그래프도 그래프로 취급된다고 합니다. 그래프는 G = (V, E)와같이 표현됩니다.
undirected graph, 무방향 그래프는 그래프를 이루는 간선의 정점들이 순서가 없는 그래프를 말합니다. directed graph, 방향 그래프는 말 그대로 방향(순서)이 있는 간선들로 이루어진 그래프를 말합니다. 그래프에는 제한이 존재하는데, 간선이 한 정점에서 같은 정점으로 돌아오는 self loop가 없어야 하며, 같은 간선이 여러 개 존재할 수 없습니다. 후자를 어기면 multigraph라는 데이터 객체를 얻습니다. 그래프는 Adjacency Matrix, Adjacency List 등의 형태로 표현됩니다. Adjacency Matrix와 Adjacency List가 어떻게 표현되는지는 위 포스팅 가장 하단의 참고 링크를 보시면 알 수 있습니다.
DFS
무방향 그래프와 그 그래프의 정점 하나가 주어졌을 때, 우리는 해당 정점에서 도달할 수 있는 모든 정점을 방문할 수 있습니다. 그러기 위한 첫 번째 방식이 바로 DFS입니다. DFS는 Depth First Search(깊이 우선 탐색)의 약자로서, 시작 정점에서 탐색을 시작하여 해당 정점에 연결되어 있으면서 아직 방문하지 않은 다른 정점을 Adjacency List 혹은 Adjacency Matrix를 통해 선택합니다. 그리고 시작 정점의 Adjacency List (인접 리스트) 혹은 Adjacency Matrix(인접 행렬)에서의 우리의 현재 위치를 스택(stack)에 저장합니다.
연결된 모든 정점을 방문했다면, 스택에서 정점을 하나 삭제한 뒤에 그것의 Adjacency List 혹은 Adjacency Matrix를 이용해 같은 과정을 반복합니다. 물론 이 과정에서 이미 방문한 정점들은 스택에 저장되지 않습니다. 탐색은 스택이 비었을 때 끝이 납니다. 실제 구현은 정점을 저장하는 스택을 선언해 준 뒤 스택을 통해 이루어질 수도 있고, 재귀적으로 이루어질 수도 있습니다. 다음의 예제 코드는 재귀 호출을 사용합니다.
#include <stdio.h>
#define FALSE 0
#define TRUE 1
short int visited[MAX_VERTICES];
typedef struct node *node_pointer;
typedef struct node{
int data;
node_pointer link;
}; //Structure for adjacency list
void dfs(int v){
/* Depth Firsh Search example */
node_pointer w;
visited[v] = TRUE; //Mark the visited vertex
printf("%d", v);
for(w=graph[v]; w; w->link) //for all vertices in v's adjacency list
if(!visited[w->vertex]) //if the vertex is not visited,
dfs(w->vertex); //recursively run depth first search for that vertex
}
Adjacency List를 사용하는 경우, DFS는 리스트의 각 정점을 최대 한 번만 방문하기 때문에 시간복잡도는 //(O(e)//)가 됩니다. e는 간선의 개수를 의미합니다. Adjacency Matrix를 사용하는 경우, 정점의 개수가 n이라고 할 때 한 정점에 인접한 모든 정점을 결정하는 데에 //(O(n)//)의 시간이 소요됩니다. 그런데 정점 n개에 대해서 이 과정을 거쳐야 하므로, 최종 시간복잡도는 //(O(n^2)//)이 됩니다.
BFS
다음으로는 BFS에 대해 알아보도록 하겠습니다. BFS는 Breadth First Search(넓이 우선 탐색)의 약자로서, 먼저 시작 정점에서 시작하여 시작 정점의 방문 여부를 표시합니다. 그런 다음 Adjacency List 혹은 Adjacency Matrix를 사용하여 시장 정점에 인접한 정점들을 방문합니다. 시작 정점에 인접한 모든 정점을 방문한 후에는, 첫 정점(시작 정점)의 Adjacency List 혹은 Adjacency Matrix에 있던 정점들의 인접 정점을 방문합니다.
이를 실제로 구현하기 위해서, 방문한 각각의 정점은 큐(queue)에 저장됩니다. Adjacency List 혹은 Adjacency Matrix에 존재하는 모든 정점을 방문한 이후에는 큐에서 정점 하나를 삭제하고 해당 정점의 Adjacency List 혹은 Adjacency Matrix에 존재하는 정점들을 검사하는 것입니다. 이 과정에서 이전에 방문하지 않았던 정점들을 방문하게 되면, 방문 여부를 변경해 주고 큐에 삽입하도록 합니다. 큐에 더 이상 정점이 존재하지 않으면 탐색은 끝이 납니다. 다음의 예제 코드는 동적으로 연결된 큐를 사용합니다.
#include <stdio.h>
#define FALSE 0
#define TRUE 1
#define MAX_VERTICES 100
short int visited[MAX_VERTICES];
typedef struct node *node_pointer;
typedef struct node{
int data;
node_pointer link;
}; //Structure for adjacency list
typedef struct queue *queue_pointer;
typedef struct queue{
int vertext;
queue_pointer link;
}; //Structure for dynamically linked queue
queue_pointer front, rear;
void addq(int);
int deletep();
void bfs(int v){
/*breadth first traversal of a graph, starting with node V.
the global array visited is initialized to 0*/
node_pointer w;
front = rear = NULL; //initialize queue
printf("%d", v);
visited[v] = TRUE; //mark starting vertex
addq(v); //insert starting vertex into queue
while(front){ //while queue is not empty
v = deleteq(); //delete vertex from queue
for(w=graph[v]; w; w->link){ //for all vertices adjacent to that vertex
if(!visited[w->vertex]){ //if the vertex is not visited
print("%d", w->vertex);
addq(w->vertex); //insert that vertex into queue
visited[w->vertex] = TRUE; //mark the vertex
}
}
}
}
각 정점이 큐에 정확히 한 번씩만 들어가게 되므로, while loop는 최대 n번 반복됩니다. Adjacency List를 사용하면 이 loop는 각 정점의 degree, 즉 각 정점에 인접한 정점의 합(각 정점에 연결된 간선의 개수)만큼의 시간복잡도를 갖게 됩니다. 따라서 이때의 시간복잡도는 //(O(e)//)가 됩니다. e는 간선의 개수를 의미합니다. Adjacency Matrix를 사용하는 경우, while loop는 방문한 각 정점에 있어 //(O(n)//)을 소요하여 해당 정점에 인접한 정점들을 결정하게 되므로 최종 시간복잡도는 //(O(n^2)//)이 됩니다.
참고
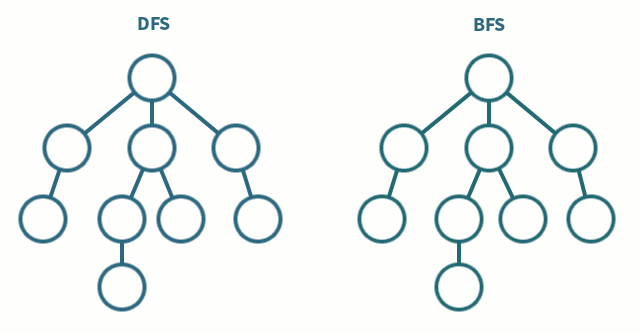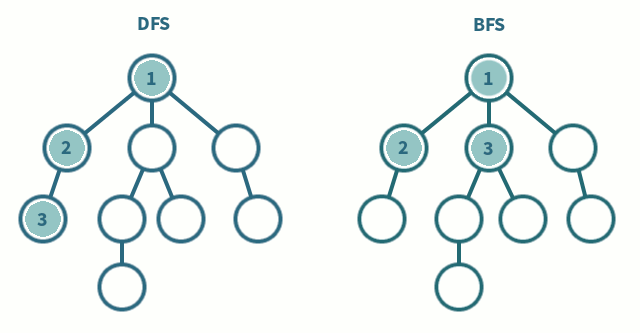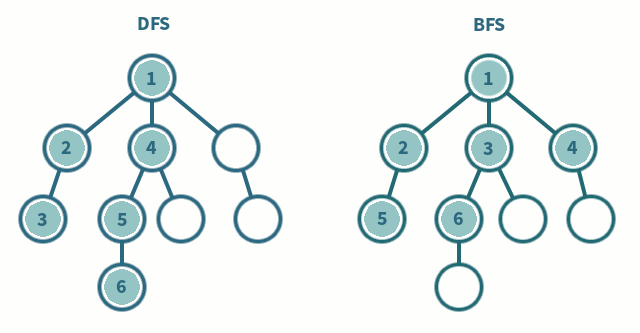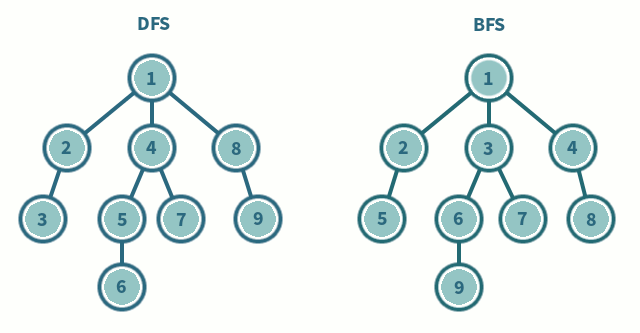
위의 움짤을 보시면 DFS와 BFS의 차이를 알 수 있습니다. 탐색하고자 하는 그래프가 많은 층으로 이루어져 있다면 DFS가 빠르게 탐색할 수 있을 것이고, 넓게 퍼진 모양의 그래프라면 BFS가 좀 더 효율적이겠죠?
추가적으로, 다음의 사이트에서는 DFS와 BFS를 시각화해서 보여 줍니다. 좀 더 직관적으로 DFS와 BFS에 대해 이해할 수 있어 도움이 많이 됐습니다. 그래프가 Adjacency List로 표현된 경우와 Adjacency Matrix로 표현된 경우를 모두 살펴볼 수 있습니다. 실제로 구현했을 때의 작동 방식을 그대로 보여 주니 직접 구현해 보기 전에 한 번씩 참고해 보시면 좋을 듯합니다.
DFS :: https://www.cs.usfca.edu/~galles/visualization/DFS.html
Depth-First Search Visualization
www.cs.usfca.edu
BFS :: https://www.cs.usfca.edu/~galles/visualization/BFS.html
Breadth-First Search
www.cs.usfca.edu
이상으로 DFS와 BFS에 대해 알아보았습니다. 질문 및 지적은 언제나 환영합니다. 다른 분들께 도움이 되었으면 좋겠네요. 영어를 그대로 한글로 번역한 느낌이 든다면... 그 느낌이 거의 맞습니다. 설명하는 글쓰기는 생각보다 어렵다는 걸 느꼈습니다. 과제 하면서 참고했던 다른 블로거 분들 모두 존경합니다. 그나저나 티스토리에 기본으로 있는 코드블럭은 안 예쁘네요. 다음부터는 다른 걸 사용해야겠습니다.
'Algorithm' 카테고리의 다른 글
| [알고리즘] 이분 매칭(Bipartite Matching) 알아보기 (0) | 2019.08.21 |
|---|---|
| [알고리즘] Prefix sum(구간 합)에 대해 알아보기 (0) | 2019.07.27 |
| 알고리즘 문제 풀이 사이트 모음(2019.07.07 ver) (3) | 2019.07.07 |


